Inequality 1

Understanding the INEQUALITY

Many mathematical techniques lend themselves to shortcuts.

Sometimes these shortcuts are great and other times

they seem to be "too tricky" to make sense when the

same type problem needs attention later.

One particular case is graphing an Open Sentence

that is an INEQUALITY.

For example:

Graph the Solution Set for   "5 <  x"

Some students are taught to always have the

"X" on the left so that the >  or < will point in the

direction of the shaded solution. This requires

the student to sometimes "SWITCH" the direction

that the inequality sign points. (This switching only

occurs when "X" is on the RIGHT SIDE!)

so "5 < x" becomes "x > 5"

the graph is  ...

The idea of 1) moving the x to the LEFT,

2) switching the direction of  "<"  to ">"

and then 3) pointing the arrow of the graph in the

direction of ">" does produce a correct graph.

My suggestion is to encourage the students

to read the inequality starting with "X".

"5 < x"

would be read "X is GREATER than 5."

Since we are graphing "X's", this method

of translation will lead to the correct

direction of the ARROW in the graph.

*******************************

You may want to get a larger view of a VIDEO.
Click on the bottom right corner.

The PLAY arrow sometimes needs to be clicked TWICE.

If you Click on an image
a LARGER view will appear.

A general discussion of 

No SOLUTION vs. All REAL NUMBERS 

(This has similar results with = EQUATIONS)

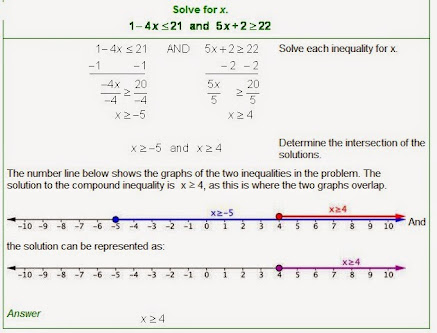
Here is a More Difficult Inequality 

where the VARIABLES completely disappear

 when we try to get them onto one side of < or > or even =

The problems below are MORE DIFFICULT.

Your class may never do this level of problem.